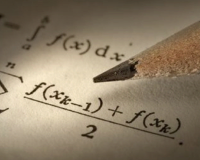quinta-feira, 29 de setembro de 2011
EU DIGO E... PROVO!!!! Parte (I).
EU DIGO E... PROVO (mermo)!!!!!
Para que as nossas afirmações tenham aceitação de verdade, devemos provar a sua eficácia, a sua veracidade através de um tipo de teste, através de alguma... prova!
A matemática é uma ciência exata, disso ninguém tem dúvidas, porém, quando se faz, ou se realiza alguma operação matemática, para termos certeza que aquela operação foi feita corretamente, devemos empregarmos um tipo de teste, uma prova para a operação realizada (adição, subtração, multiplicação ou divisão) tipo: prova real ou prova dos noves fora.
Antes de começar a mostrar como se faz essas provas para cada uma daquelas operações citadas, eu quero chamar a atenção do leitor, para o nosso sistema de contagem, ou seja: o sistema decimal.
O mesmo consta de usarmos a base de contagem de dez em dez unidades em todas as classes e em todas as ordens que são constituintes de qualquer número escrito.
Além disso, o sistema decimal é um... sistema posicional. Isto significa que: cada algarismo lançado no número terá dois valores, a saber: valor absoluto ( V. A.) que é o dele mesmo, em qualquer ordem em que ocupar e... valor relativo ( V. R.) que dependerá da ordem em que ele esteja ocupando.
Para formarmos um número, começamos a lançar os valores a partir das ordens colocadas mais à direita e as classes também. Veja isto:
Exemplo da formação das centenas:
000 001 002 003 004 005 006 007 008 009
010 011 012 013 014 015 016 017 018 019
020 021 022 023 024 025 026 027 028 029
030 031 032 033 034 035 036 037 038 039
040 041 042 043 044 045 046 047 048 049
050 051 052 053 054 055 056 057 058 059
060 061 062 063 064 065 066 067 068 069
070 071 072 073 074 075 076 077 078 079
080 081 082 083 084 085 086 087 088 089
090 091 092 093 094 095 096 097 098 099
100 101 102 103 104 105 106 107 108 109 110 111 112 113 ...
e assim em diante!
A leitura de um número:
Vou através de exemplos numéricos, tornar compreensível o que acabo de falar.
Seja o número: 23 598 423 685 005 540 e ele possui:
6 classes, sendo 5 classes completas com os três algarismos e uma incompleta com 2 algarismos;
começamos denominando as classes no sentido da direita para a esquerda, assim:
Unidades simples; milhares; milhões; bilhões; trilhões e... quatrilhões.
Agora, de posse dessas informações, tomando-se o sentido inverso, lê-se por extenso o valor absoluto do número dado, como: vinte e três quatrilhões, quinhentos e noventa e oito trilhões, quatrocentos e vinte e três bilhões, seiscentos e oitenta e cinco milhões, cinco mil e quinhentos e quarenta unidades.
Operações fundamentais:
Número é ideia de quantidade e, para representar essas quantidades, fazemos uso dos numerais falados e escritos.
E para um maior domínio, utilizamos os algarismos, que são sinais gráficos especiais (símbolos) que são combinados entre si, através das regras da contagem para permitir-nos representar as quantificações das grandezas e também de operá-las.
São muitas as operações já inventadas pelo ser humano, mas, no acervo delas encontramos quatro, que são chamadas de... operações fundamentais e que são: adição, subtração, multiplicação e a divisão.
São as operações matemáticas mais utilizadas por nós e são ditas fundamentais ( Principalmente a soma e a subtração) porque, mesmo que estejamos trabalhando com uma operação complexa, a toda instante, se prestarmos atenção, percebemos o uso dessas operações mais simples para terminar a tarefa com aquela.
As provas operatórias:
Então, essas operações mais simples, fundamentais, muito utilizadas no cálculo exige também, que sejamos precisos no seu manoseio e aí, temos que saber realizar ao finalizar cada uma delas, a aplicação de um teste, de preferência, que seja simples e rápido, para a confirmação do resultado obtido. São as chamadas... prova real e a prova dos noves fora.
A chamada, prova real, dependendo da operação empregada, poderá ser alguma propriedade constituinte dessa operação ou a obtensão do valor de um dos seus termos, através de uma equação.
Já a prova dos noves fora, é baseada na regra da contagem do sistema decimal e posicional, de base dez, que determina que em nenhuma posição ou ordem de um número, possamos colocar um valor acima de nove e, daí vem o nome... prova dos noves fora, na realidade isto que dizer: devemos obter o resto da divisão de um número inteiro pelo número nove!
É aplicada nos termos da operação usada, para obtermos outros valores que serão novamente operados e dependendo do resultado final, onde, em se tendo valores iguais na confrontação, deduzimos o acerto ou não na operação.
Eu digo e... provo que acertei o resultado de uma ADIÇÃO, quando, por exemplo:
sejam dados os números... 216587121665, 120000546571, 2455101 e 25132812 e pede-se a soma dos mesmos, então eu faço:
216587121665 1ª parcela
120000546571 2ª parcela
2455101 3ª parcela
+ 25132812 4ª parcela
___________________
336615256149 Soma ou Total.
Agora, vem a pergunta, esse resultado está certo? É confiável?
Então, para isto , vamos fazer a prova real da adição, que nada mais é, do que o uso de uma das propriedades da soma, a Propriedade Comutativa da Adição que determina: “ a ordem das parcelas não altera a soma ou total”!
Então, o que vamos fazer é, simplesmente, somarmos no sentido vertical que fizemos, isso mesmo, vamos somar “ de baixo para cima...
336615256149 Soma ou Total.
_____________________________
216587121665 1ª parcela
120000546571 2ª parcela
2455101 3ª parcela
+ 25132812 4ª parcela
___________________
336615256149 Soma ou Total.
E veja: achamos o mesmo resultado! Como é muito difícil, errarmos duas vezes seguidas, assim eu posso dizer que 336615256149 Soma ou Total do início, é correto!
A Prova Real, realmente, podemos confiar no seu veredicto. Porém, mais demorada para se fazer, uma vez que temos de repetir a operação. Temos um outro tipo de prova com resultado mais rápido de ser obtido, mas essa prova, ao contrário da primeira, não é muito confiável e , já sabe.
Trata-se da … Prova dos Noves Fora e que repetindo o que dissera antes, é um processo em que se obtém o resto da divisão de um número inteiro pelo número nove, ser ser preciso, de fato, realizar a divisão propriamente dita! Vamos desfazer... o mistério?
Tome um número inteiro, por exemplo: 35498651685215 e eu quero saber, qual é o resto da divisão desse número por 9 mas, sem ser preciso fazer a divisão. Vamos lá:
vamos da esquerda para a direita, somando um à um, os dígitos dese número mas deixando de fora tanto os zeros quanto os noves. Certo?
E à medida que formos obtendo as somas dos outros algarismos, quando se tiver um valor igual ou maior que o nove, devemos obtermos o resto da divisão desse valor pelo número nove e continuamos até o final.
Bem, trocando em miúdos, vamos ao exemplo prático:
de... 35498651685215... façamos... 3 + 5 + 4 + 9 + 8 + 6 + 5 + 1 + 6 + 8 + 5 + 2 + 1+ 5 e somamos...
==> 3 + 5 = 8! (Atenção! 8! não é fatorial do número, isto foi só para chamar a atenção!).
==> 8 + 4 = 12 doze é maior do que 9 e... 12 : 9 = 1 com resto 3!
Ou podemos obter este resultado fazendo... 12 noves fora igual ==> 1 + 2 = 3 (macete)! Bom, com esse resto igual a 3, continuamos com o próximo algarismo… o 8 (antes tinha o 9, que não se considera), então...
==> 8 + 4 = 12 e 1 + 2 = 3! ( 12: 9 = 1 com resto 3!) e continua-se:
==> 3 + 8 = 11 e 1 + 1 = 2! ( 11: 9 + 1 com resto 2!) e continua-se:
==> 2 + 6 = 8! (já sabe, não é?)
==> 8 + 5 = 13 e 1 + 3 = 4! (já sabe, não é?)
==> 4 + 1 = 5!
==> 5 + 6 = 11 e 1 + 1 = 2!
==> 2 + 8 = 10 e 1 + 0 = 1!
==> 1 + 5 = 6!
==> 6 + 2 = 8!
==> 8 + 1 = 9 e 9 noves fora 0! ( 9 : 9 = 1 com resto igual a zero! Matou?)
==> 0 + 5 = 5! noves fora final, isto quer dizer que o resto da divisão do número 35498651685215 pelo nove é igual a 5. ( 35498651685215 : 9 = 3944294631690 com resto 5!). Pode conferir!
Podemos realizar isso com os termos da adição, para se saber se fizemos tudo certo! Vamos ver?
Seja a soma realizada...
216587121665 1ª parcela
120000546571 2ª parcela
2455101 3ª parcela
+ 25132812 4ª parcela
___________________
336615256149 Soma ou Total.
1º) traçamos uma pequena linha horizontal, preferencialmente, à direita da conta armada, e vamos achar os noves fora das parcelas.
216587121665 1ª parcela
120000546571 2ª parcela
2455101 3ª parcela
+ 25132812 4ª parcela _____________
___________________
336615256149 Soma ou Total.
2º) Na parte de cima da linha, traçada agora, vamos colocar o valor dos noves fora, assim como fizemos com o número... 336615256149, encontrado com as parcelas, dígito após dígito, uma parcela após a outra e desse modo, vamos achar... 6!
Portanto, lançamos... o 6 acima da linha.
216587121665 1ª parcela
120000546571 2ª parcela
2455101 3ª parcela 6
+ 25132812 4ª parcela _____________
___________________
336615256149 Soma ou Total.
3º) Achamos agora os noves fora da soma ou total... encontraremos, também um 6!
E lançamos abaixo da linha e desse modo temos:
216587121665 1ª parcela
120000546571 2ª parcela
2455101 3ª parcela 6
+ 25132812 4ª parcela _____________
___________________
336615256149 Soma ou Total. 6
4º) Confrontamos os resultados e como são iguais, concluímos que a soma fora realizada corretamente!
Continuação em... “EU DIGO e... PROVO!!!!! Parte (II).